«آزمون فریدمن» (Friedman Test) یک «آزمون ناپارامتری آماری» (Non-Parametric Statistical Test) است که برای مقایسه شاخص‌های مرکزی چندین جامعه به کار می‌رود:

این آزمون، مشابه «تحلیل واریانس یک طرفه» (One-way  ANOVA) است که در محیط ناپارامتری اجرا می‌شود. از آنجایی که «میلتون فریدمن» (Milton Friedman) اقتصاددان آمریکایی، در سال ۱۹۳۷ برای اولین بار چنین روشی را مورد بررسی قرار داد، این آزمون را به نام او می‌شناسند.

آزمون فریدمن در SPSS

قبل از هر چیز بهتر است نحوه عملکرد آزمون فریدمن و آماره آزمون آن را مشخص کنیم. برای اجرای این آزمون، یک جدول اطلاعاتی در نظر گرفته، سپس آماره آزمون فریدمن را براساس رتبه مقادیر رتبه‌ها در هر سطر با رتبه‌های ستونی محاسبه می‌شود. به این ترتیب این آزمون در «طرح‌های بلوکی کامل» (Complete Block Design) بسیار به کار می‌رود. به یک مثال در این زمینه توجه کنید.

n جوشکار از k نوع الکترود جوشکاری استفاده می‌کنند و جوش‌های اجرا شده براساس کیفیت رتبه‌بندی (امتیاز) می‌شوند. آیا می‌توان الکترودی را بهتر از بقیه تشخیص داد یا همه آن‌ها در جوشکاری، نقش یکسانی دارند؟ توجه داشته باشید که هر جوشکار، از همه k نوع الکترود برای سنجش، استفاده کرده است.

اگر از توزیع کیفیت (رتبه) کار این الکترودها اطلاعاتی نداشته باشیم، باید یک روش ناپارامتری (Nonparametric method) به کار ببریم و الکترودی را بهتر از بقیه بشناسیم که برای همه n جوشکار، رتبه بهتری ارائه کرده است. به نظر می‌رسد که این آزمون درست به مانند «تحلیل واریانس با مقادیر تکراری» (One-way Repeated Measures Analysis of Variance) در حالت پارامتری است که به جای مقادیر از رتبه‌های آن‌ها استفاده می‌شود.

در این آزمون، فرض صفر یکسان بودن تیمارها و فرض مقابل، نابرابری حداقل یکی از تیمارها با بقیه در نظر گرفته می‌شود.

آماره آزمون فریدمن

یک ماتریس داده به صورت $$\{x_{ij}{\}}_{n\times k}$$

در نظر بگیرید. واضح است که این ماتریس دارای $$n$$ سطر یا بلوک (Block) و $$k$$

ستون یا «تیمار» (Treatment) است. مقادیر مشاهدات در این ماتریس نیز «رتبه» (Rank) مقدار برجسب هر بلوک یا سطر است.

نکته: اگر رتبه‌ها دارای گره (Tie) باشند، میانگین رتبه‌ها ملاک قرار می‌گیرد. به این ترتیب در ماتریس گفته شده، رتبه‌ها، جایگزین مقادیر شده و یک ماتریس به صورت $$\{r_{ij}{\}}_{n\times k}$$

ساخته می‌شود که هر درایه‌ آن، مثل $$r_{ij}$$، رتبه مقدار $$x_{ij}$$ درون بلوک یا سطر $$i$$

است.

میانگین رتبه‌ها را برای ستون $$j$$

به صورت زیر محاسبه می‌کنیم.

$${\overline{r}}_{\cdot j}=\frac{1}{n}\sum _{i=1}^n{r}_{ij}$$

با در نظر گرفتن متوسط رتبه‌های حاصل، آماره آزمون فریدمن که با نماد $$Q$$

نشان داده می‌شود، به صورت زیر خواهد بود.

$$Q=\frac{12n}{k(k+1)}\sum _{j=1}^k{({}_{\cdot j}–\frac{k+1}{2})}^2$$

آماره آزمون فریدمن، در صورت بزرگ بودن $$k$$

‌ و $$n$$ (مثلا $$k\ge \mathrm{۳}$$ و $$n\ge \mathrm{۱۵}$$) به صورت تقریبی دارای «توزیع کای ۲» (Chi-squared Distribution) با $$k-\mathrm{۱}$$

درجه آزادی خواهد بود. به این ترتیب مقدار احتمال (p-value) به شکل زیر محاسبه خواهد شد.

$$P({\chi }_{k–\mathrm{۱}}^{\mathrm{۲}}\ge Q)$$

در صورتی که $$k$$

و $$n$$

کوچک باشند، این تقریب، ضعیف شده و باید مقدار احتمال را براساس جدول‌های آزمون فریدمن استخراج کرد. واضح است که در صورت معنی‌دار بودن مقدار احتمال، فرض صفر که بیانگر یکسان بودن تیمارها است را رد می‌کنیم.

در صورتی که فرض صفر رد شود، می‌توان از آزمون‌های دنباله‌ای یا «تعقیبی» (Pos-Hoc) کمک گرفت و مشخص کردن تفاوت بین کدام تیمار وجود دارد.

آزمون‌های مرتبط با آزمون فریدمن

اگر داده‌ها مربوط به مقادیر «دو وضعیتی» (Binary Response) باشند، به جای آزمون فریدمن می‌توان، «آزمون Q کاکران» (Cochran’s Q test) را اجرا کرد. همچنین آماره W کندال (Kendall’s W) حالت نرمال شده آماره آزمون فریدمن در بازه ۰ تا ۱ است. به این ترتیب می‌توان این دو آزمون را در این حالت، معادل در نظر گرفت. از طرفی «آزمون رتبه‌ علامت‌دار ویلکاکسون» (Wilcoxon Signed-rank Test) برای زمانی که دو گروه یا متغیر وابسته به یکدیگر باشند نیز به عنوان جایگزین آزمون فریدمن به کار می‌رود.

خوشبختانه آزمون فریدمن در بیشتر نرم‌افزارهای محاسبات آماری قابل اجرا است. در ادامه به نحوه اجرای آزمون فریدمن در SPSS خواهیم پرداخت.

چیدمان داده‌ها و تفسیر آزمون فریدمن در SPSS

همانطور که گفته شد، برای حالتی که بیش از سه جامعه مستقل وجود داشته و قرار است برابری میانگین آن‌ها بوسیله مقادیر تکراری مورد بررسی قرار گیرد، «تحلیل واریانس با مقادیر تکراری» (Repeated Measures ANOVA) بهترین گزینه است. ولی اگر تعداد مشاهدات کم بوده و نتوان توزیع نرمال را برای مقادیر اندازه‌گیری شده در نظر گرفت، به آزمون ناپارامتری فریدمن اکتفا خواهیم کرد.

در تصویر ۱، نمونه‌ای از مشاهدات ثبت شده در SPSS را می‌بینید که براساس سه تیمار (یا نحوه امتیاز دهی) مقدار دهی شده‌اند. سوال این است که آیا میانگین این سه جامعه (تیمار) برابر است یا خیر؟

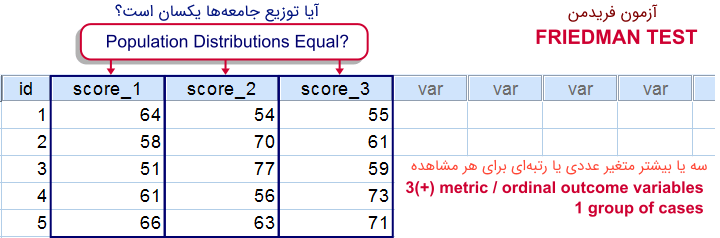
همانطور که می‌بینید، از هر فرد سه بار اندازه‌گیری صورت گرفته و نظرشان براساس امتیاز از ۱ تا ۱۰۰ برای سه نوع تیمار تحت متغیرهای score_1 تا Score_3 ملاک قرار گرفته است.

به منظور محاسبه آماره آزمون، رتبه هریک از پاسخ‌ها در سطر، به کار می‌رود. در تصویر ۲، رتبه‌های هر یک از مقادیر نسبت به هر سطر مشخص شده و برای محاسبه آماره آزمون به کار رفته است. این نتایج را در تصویر زیر در بخش شماره ۱ می‌بینید. از طرفی میانگین رتبه (Mean Rank) هر ستون یا متغیر نیز در جدول رتبه‌ها (Ranks) قرار گرفته که در بخش شماره ۲ قابل مشاهده است. مقدار آماره آزمون (Chi-square) و درجه آزادی و همچنین مقدار احتمال (.Asymp. Sig) نیز در جدول Test Statistics (بخش ۳ و ۴) دیده می‌شود.

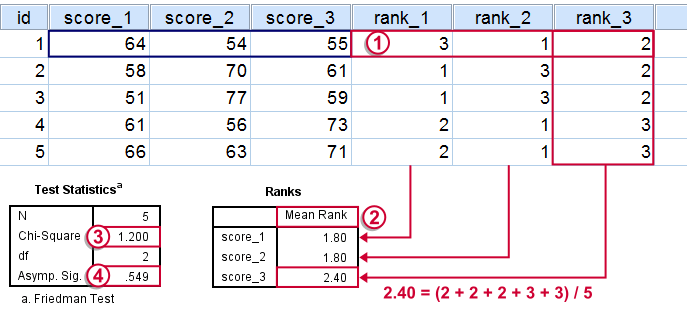
اطلاعات مربوط به بخش‌های شماره‌گذاری شده در تصویر ۲، در ادامه توصیف شده‌اند.

1. رتبه‌های اصلی محاسبه شده براساس مقادیر متغیرها در کاربرگ SPSS محاسبه شده‌اند. دقت کنید که رتبه هر مقدار با توجه به مقادیر همان سطر تعیین می‌شود. برای مثال از آنجایی که در سطر اول ۵۴ کوچکترین مقدار در بین متغیرها است، رتبه اول را بدست آورده.
2. میانگین رتبه‌ها برای هر متغیر به کمک جمع رتبه‌های هر ستون حاصل می‌شود. کافی است نتیجه این جمع را بر تعداد سطرها تقسیم کنیم. تحت فرض صفر (یکسان بودن توزیع یا میانگین تیمارها) باید میانگین رتبه‌های مربوط به متغیرها با یکدیگر تفاوت چندانی نداشته باشند.
3. آماره آزمون Chi-Square در این جدول به مانند واریانس تحت میانگین رتبه‌ها عمل می‌کند هر چه مقدار این آماره بزرگتر باشد، تفاوت در رتبه‌ها بیشتر است. چنانچه تفاوت بین میانگین‌ها صفر باشد یا مقدار Chi-Square کوچک باشد، هر سه متغیر دارای توزیع یا میانگین یکسانی هستند. در نتیجه، تیمارها بی‌اثر بوده و عملکرد یکسانی خواهند داشت.
4. مقدار .Asymp. Sig همان مقدار احتمال است که براساس توزیع مجانبی یا تقریبی حاصل شده. از آنجایی که این مقدار از «احتمال خطای نوع اول» ($$\alpha =\mathrm{۰٫۰۵}$$

4. ) بزرگتر است، دلیلی بر رد فرض صفر وجود ندارد. پس به نظر می‌رسد که تیمارها بی‌اثر بوده یا متغیرها دارای توزیع یکسانی هستند.

اجرای آزمون فریدمن در SPSS

این بار براساس یک فایل داده، آزمون فریدمن را در SPSS اجرا می‌کنیم تا نحوه به کارگیری این آزمون را در SPSS فرا گرفته و آن را به کار ببندیم. فرض کنید، در یک مجموعه داده، امتیاز به آگهی‌های بازرگانی برای خرید سه نوع خودرو، ثبت شده است. هر یک از مشتریان، به هر سه نوع آگهی امتیازی بین ۰ تا ۱۰۰ داده‌اند. می‌خواهیم ببینیم آیا این افراد نسبت به آگهی‌ها نظر خاصی دارند یا اینکه همه آن‌ها یک اثر بر بیننده یا خواننده می‌گذارند و در نتیجه مشاهده آن‌ها با یکدیگر تفاوت معنی‌داری ندارد.

به منظور دسترسی به این فایل داده به نام adratings.sav، کافی است از اینجا فایل فشرده را دریافت کرده، پس از خارج کردن از حالت فشرده، آن را در «پنجره ویرایشگر داده» (Data Editor) بارگذاری و نمایش دهید. تعداد شرکت کنندگان در این تحقیق ۱۸ نفر است که امتیاز آن‌ها به سه نوع آگهی تبلیغاتی ماشین در متغیرهای ad1, ad2 و ad3 ثبت شده است.

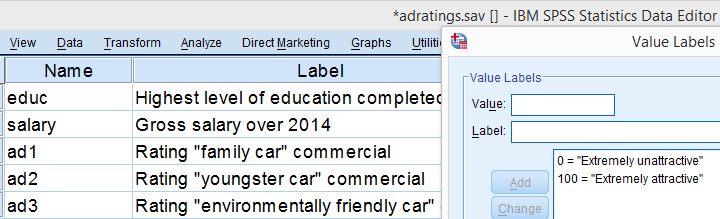
در تصویر ۳، نمونه‌ای از کد گذاری رتبه‌ها را برای دو مقدار ۰ (کاملا غیر جذاب-Extremely Unattractive) و ۱۰۰ (بسیار جذاب-Extremely Attractive) مشاهده می‌کنید. می‌خواهیم بدانیم که آیا واقعا نوع آگهی در معرفی خودرو و جلب نظر مشتریان، تفاوت معنی‌داری ایجاد می‌کند یا خیر. پس توجه داشته باشید که در اینجا، فرض صفر به این صورت بیان می‌شود: «توزیع جامعه برای سه نوع رتبه‌بندی یکسان است.»

بهتر است، ابتدا شرایط اجرای آزمون فریدمن را مورد بررسی قرار دهیم.

بررسی نرمال بودن داده‌ها

همانطور که می‌دانید، اگر داده‌ها، شرایط به کارگیری آزمون‌های پارامتری مانند نرمال بودن توزیع را داشته باشند، ارجح است که از آن‌ها استفاده کنیم. بنابراین ابتدا مجموعه داده adratings را از لحاظ نرمال بودن متغیرها، بررسی می‌کنیم.

یک راه ساده برای نمایش توزیع هر یک از این متغیرها، رسم نمودار فراوانی و مطابقت آن با توزیع نرمال است. کافی است از مسیر زیر اقدام کرده و جدول فراوانی و نمودار فراوانی متغیرها مورد نظر را رسم کنیم.

Analyze >  Descriptive Statistics > Frequencies

نکته: به منظور اجرای فرمان بالا در محیط کد نویسی SPSS از دستورات زیر در پنجره Syntax استفاده کنید.

نتیجه اجرای این دستور برای متغیر ad2 با برچسب Rating “youngster car” commercial به مانند تصویر ۴، خواهد بود.

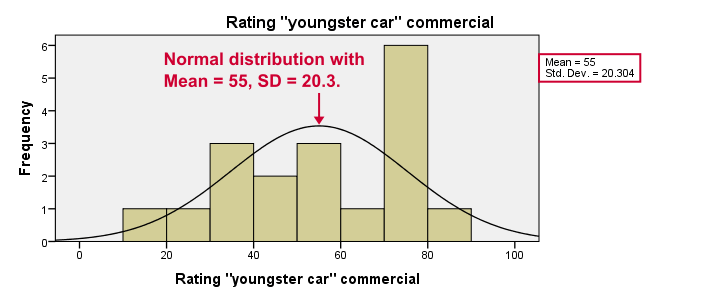
واضح است که منحنی فراوانی (نمودار ستونی) با توزیع نرمال (منحنی نمایش داده شده) مطابقت ندارند. بنابراین نمی‌توان از توزیع نرمال برای توصیف جامعه آماری بهره برد و به ناچار باید روش‌های ناپارامتری برای آزمون مقایسه میانگین یا توزیع سه جامعه را به کار گیریم.

اجرای آزمون فریدمن در SPSS برای مجموعه داده adrating

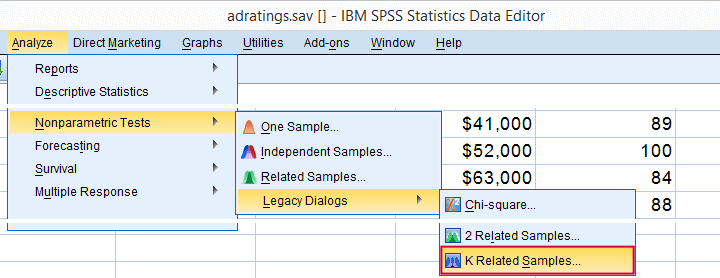
به منظور اجرای آزمون فریدمن در SPSS از مسیری که در تصویر ۵، دیده می‌شود، اقدام کنید. از آنجایی که با سه تیمار (بیش از دو متغیر) مواجه هستیم، گزینه «K-Related Samples» را انتخاب کرده‌ایم.

به این ترتیب پنجره دریافت پارامترهای این آزمون مطابق با تصویر ۶، ظاهر می‌شود. کافی است تنظیمات را به مانند این تصویر انجام دهید. همانطور که مشاهده می‌کنید، متغیرهایی که در آزمون مورد استفاده قرار گرفته‌اند، امتیازات یا رتبه‌های مشتریان به سه نوع آگهی است.

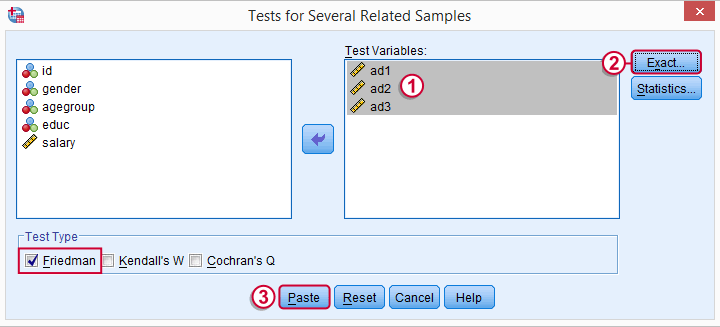
در قسمت انتخاب نوع آزمون (test Type)، گزینه Friedman را انتخاب کنید. اگر می‌خواهید آزمون دقیق با توجه به توزیع واقعی آماره آزمون فریدمن صورت گیرد، دکمه Exact را کلیک کرده و پارامترهای آن را مطابق با تصویر ۷، اجرا کنید.

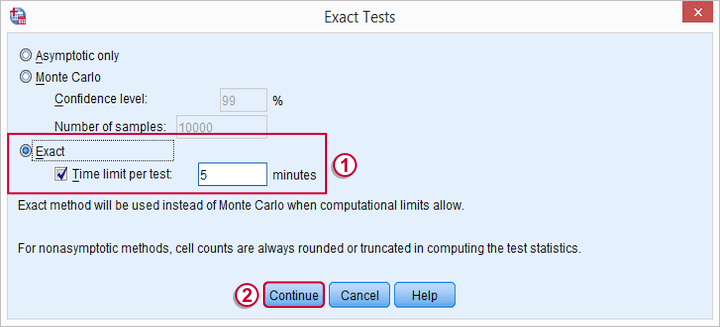
از آنجایی که به کارگیری آزمون دقیق، برای داده‌های حجیم، ممکن است زمان‌بر باشد، بهتر است پارامتر آزمون دقیق یعنی حداکثر «زمان انتظار برای اجرا» (Time limit per test) را وارد کنید. این زمان به طور پیش‌فرض، ۵ دقیقه در نظر گرفته شده است. البته توجه داشته باشید که در بیشتر مواقع، زمانی از آزمون Exact استفاده می‌شود که حجم نمونه‌ها یا تعداد متغیرها کم باشند. در نتیجه توزیع آماره آزمون باید به شکل دقیق به شیوه‌ای که فریدمن معرفی کرده، تعیین شود.

با فشردن دکمه Continue و بازگشت به پنجره اصلی، کافی است اجرای آزمون را با کلیک روی دکمه OK‌، تایید کنید. با فشردن دکمه Paste، کد مربوط به اجرای این فرمان در پنجره Syntax قرار خواهد گرفت.

نکته: اگر می‌خواهید در محیط کد نویسی SPSS، فرمان آزمون فریدمن را اجرا کنید، دستورات زیر را در پنجره Syntax وارد کرده و آن‌ها را اجرا نمایید.

تفسیر خروجی آزمون فریدمن در SPSS

در تصویر ۸، نتیجه اجرای آزمون فریدمن در SPSS را برای مجموعه داده adrating.sav مشاهده می‌کنید.

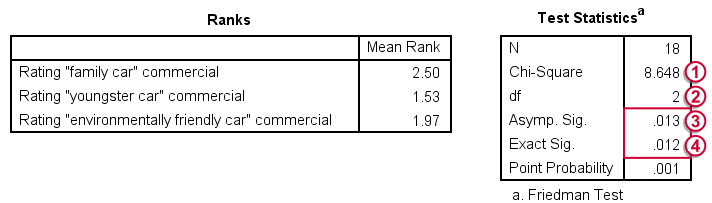
از آنجایی که مقدار «آماره مربع کای» (Chi-Square) با درجه آزادی ۲، بزرگ به نظر می‌رسد و مقدار احتمال، چه مجانبی (۰٫۱۳ =.Asymp. Sig) و چه دقیق (۰٫۰۱۲=.Exact Sig) از احتمال خطای نوع اول $$\alpha =\mathrm{۰٫۰۵}$$

کوچکتر هستند، رای به رد فرض می‌دهیم. به این معنی که به نظر می‌رسد نوع آگهی در امتیاز مشتریان تاثیر گذار است. این موضوع بیانگر آن است که حداقل یکی از آگهی‌ها میزان رضایت بیشتری نسبت به بقیه در مخاطبان ایجاد کرده است ولی مشخص نیست این کدام آگهی است.

برای آن که مشخص کنیم کدام آگهی اثر بخشی متفاوتی نسبت به سایر موارد دارد، باید آزمون‌های مقایسه‌های دوتایی (با حفظ سطح خطا) را اجرا کنیم که اغلب به نام «پس‌آزمون‌ها» (Post-Hoc) یا آزمون‌های تعقیبی شناخته شده هستند. در آینده، طی نوشتار دیگری از مجله فرادرس، به این نوع آزمون‌ها اشاره خواهیم کرد.

ضعف‌ها و قوت‌های آزمون فریدمن

هر چند آزمون فریدمن احتیاجی به اطلاع از توزیع مقادیر متغیرها ندارد، ولی اگر توزیع آن‌ها نرمال یا نزدیک به نرمال باشد، توان آزمون مربوط به جدول تحلیل واریانس (ANOVA) به عنوان یک روش پارامتری، بیشتر از آزمون فریدمن است. متاسفانه برای انجام آزمون فریدمن، لازم است که همه متغیرها یا تیمارها دارای تعداد مشاهدات یکسان و برابری باشند. این موضوع نیز یکی از ضعف‌های عمده برای چنین آزمونی محسوب می‌شود.

در زمانی که مسئله یک «طرح بلوکی متوازن» (Balanced Block Design) باشد، آزمون فریدمن بهترین کارایی را با توجه به کم بودن مشاهدات خواهد داشت. با توجه به عدم شناخت از توزیع مقادیر، دقت آزمون فریدمن با در نظر گرفتن مشاهدات تکراری، از دیگر آزمون‌های مشابه بیشتر است.

خلاصه و جمع‌بندی

در این نوشتار به بررسی آزمون فریدمن در SPSS پرداختیم و خروجی‌های آن را نیز تفسیر کردیم. در این بین نحوه عملکرد این آزمون و آماره مربوطه را هم مورد بررسی قرار داده و ضعف‌ها و برتری‌های چنین آزمونی را نیز معرفی کردیم. زمانی که حجم مشاهدات کمتر از حدی باشد که بتوان توزیع آن‌ها را نرمال در نظر گرفت، آزمون فریدمن می‌تواند جایگزینی برای تحلیل واریانس باشد. البته زمانی که چولگی متغیرها نیز زیاد باشند، بهتر است از آزمون‌های ناپارامتری نظیر آزمون فریدمن، استفاده کرد.

منبع : https://blog.faradars.org